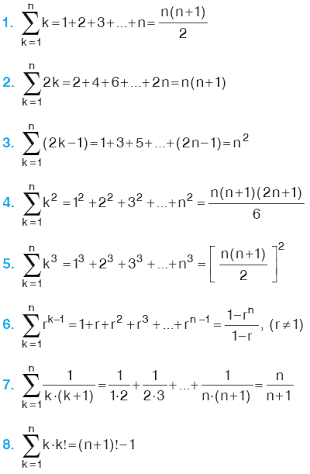1 2 2 2 3 2 N 2 Formula

Using the method of color blue proof by induction this involves the following steps prove true for some value say n 1 assume the result is true for n k. 5 0 5 0. Observe that tex k 1 3 k 3 3k 2 3k 1 tex.

blugi scurti barbati dsquared blugi levis 511 barbati blugi negrii dama bershka blugi scurti dama cu talie inalta blugi cu talie joasa dama blugi levis 501 dama blugi h m barbati blugi dama marimi mari

Algebra Ii For Dummies Cheat Sheet Algebra Math Methods Math

Summation Formulas Physics And Mathematics Science Formulas

Simplifying Factorials With Variables Algebra Lessons

Definite Integrals Math Formula Chart Learning Math Negative

Trigonometric Identities Studying Math Math Formulas Maths

Pin By Alexis Tuggle On Mathematics Studying Math Math Formulas

Here is one method to derive the formula for the sum of squares which can be extended to other integer powers.

1 2 2 2 3 2 n 2 formula. For math science nutrition history. We know that x 1 3 x 3 3x 2 3x 1. N 2 f n f 0 n n 1 2n 1 6. Imho this fact is a coincidence.

1 2 2 2 3 2. For example 1 2 2 2 10 2 10 11 21 6 385. Each of these series can be calculated through a closed form formula. If this kind of cancellation occurs in a sum it is called a telescoping sum this can be a very useful trick to know in some contexts.

This equation was. The partial sums of the series 1 2 3 4 5 6 are 1 3 6 10 15 etc the nth partial sum is given by a simple formula. Putting x 1 2 n we get. Frequently asked questions how do you find the sum of square numbers.

This result is usually proved by a method known as mathematical induction and whereas it is a useful method for showing that a formula is true it does not offer any insight into where the formula comes from. 1 2 cdots k frac k k 1 2 the corresponding claim to prove is. 1 2 3 4 5 n total n n 1 2 1 2 2 2 3 2 n 2 total n n 1 2n 1 6 1 3 2 3 3 3 4 3 n 3 total n n 1 2 2. Compute answers using wolfram s breakthrough technology knowledgebase relied on by millions of students professionals.

The problem is to find the function f n for which f n f n 1 is a in this case it is given to you. . The sum of the first n squares 1 2 2 2 n 2 n n 1 2n 1 6. The case a 1 n 100 a 1 n 100 a 1 n 1 0 0 is famously said to have been solved by gauss as a young schoolboy.

1 3 2 3 cdots k 3 frac k 2 k 1 2 4. Given the tedious task of adding the first 100 100 1 0 0 positive integers gauss quickly used a formula to calculate the sum of 5050. A better approach is to prove the closed form formula for both.